逻辑回归算法 -- 二分类

在分类问题中，我们要预测的变量 $y$ 是离散的值，我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法，这是目前最流行使用最广泛的一种学习算法。

分类问题

在分类问题中，我们尝试预测的是结果是否属于某一个类（例如正确或错误）。分类问题的例子有：判断一封电子邮件是否是垃圾邮件等。

我们将因变量(dependent variable)可能属于的两个类分别称为负向类（negative class）和正向类（positive class），

则因变量 $y\in { 0,1 \\}$，其中 0 表示负向类，1 表示正向类。

逻辑回归算法是分类算法，它适用于标签 $y$ 取值离散的情况，如：1 0 0 1。

假说表示

在分类问题中，要用什么样的函数来表示我们的假设。我们希望分类器的输出值在0和1之间，因此，我们想出一个满足某个性质的假设函数，这个性质是它的预测值要在0和1之间。

我们引入一个新的模型，逻辑回归，该模型的输出变量范围始终在0和1之间。 逻辑回归模型的假设是：$h_\theta \left( x \right)=g\left(\theta^{T}X \right)$  其中：$X$  代表特征向量，$g$  代表逻辑函数（logistic function)，一个常用的逻辑函数为S形函数（Sigmoid function），公式为：$g\left( z \right)=\frac{1}{1+{{e}^{-z}}}$ 。

python代码实现：

import numpy as np

def sigmoid(z): 

   return 1 / (1 + np.exp(-z))

该函数的图像为：

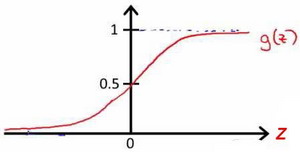
逻辑回归模型的假设：

$h_\theta \left( x \right)$ 的作用是，对于给定的输入变量，根据选择的参数计算输出变量=1的可能性（estimated probablity）即 $h_\theta \left( x \right)=P\left( y=1|x;\theta \right)$ 例如，如果对于给定的 $x$，通过已经确定的参数计算得出 $h_\theta \left( x \right)=0.7$，则表示有70%的几率 $y$ 为正向类，相应地 $y$ 为负向类的几率为1-0.7=0.3。

决策边界(decision boundary)

在逻辑回归中，我们预测：

当 ${h_\theta}\left( x \right)>=0.5$ 时，预测 $y=1$。

当 ${h_\theta}\left( x \right)<0.5$ 时，预测 $y=0$ 。

假设我们的数据呈现这样的分布情况，怎样的模型才能适合呢？

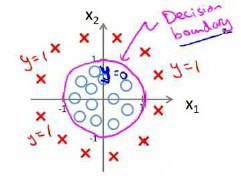
因为需要用曲线才能分隔 $y=0$  的区域和 $y=1$  的区域，我们需要二次方特征：${h_\theta}\left( x \right)=g\left( {\theta_0}+{\theta_1}{x_1}+{\theta_{2}}{x_{2}}+{\theta_{3}}x_{1}^{2}+{\theta_{4}}x_{2}^{2} \right)$ 是 -1 0 0 1 1，则我们得到的判定边界恰好是圆点在原点且半径为1的圆形。

我们可以用非常复杂的模型来适应非常复杂形状的判定边界。

代价函数

监督学习问题中的逻辑回归模型的拟合问题。

对于线性回归模型，代价函数是所有模型误差的平方和。理论上来说，我们也可以对逻辑回归模型沿用这个定义，但是问题在于，当我们将 ${h_\theta}\left( x \right)=\frac{1}{1+{e^{-\theta^{T}x}}}$ 带入到这样的代价函数中时，得到的代价函数将是一个非凸函数（non-convexfunction）。 

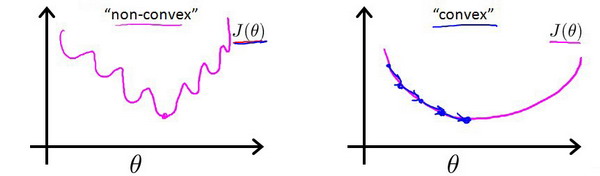
这意味着我们的代价函数有许多局部最小值，这将影响梯度下降算法寻找全局最小值。

线性回归的代价函数为：$J\left( \theta  \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{\frac{1}{2}{{\left( {h_\theta}\left({x}^{\left( i \right)} \right)-{y}^{\left( i \right)} \right)}^{2}}}$ 。

重新定义逻辑回归的代价函数为：$J\left( \theta  \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{{Cost}\left( {h_\theta}\left( {x}^{\left( i \right)} \right),{y}^{\left( i \right)} \right)}$，其中

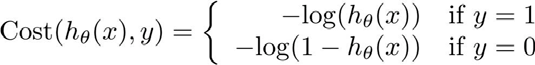
${h_\theta}\left( x \right)$ 与 $Cost\left( {h_\theta}\left( x \right),y \right)$ 之间的关系如下图所示：

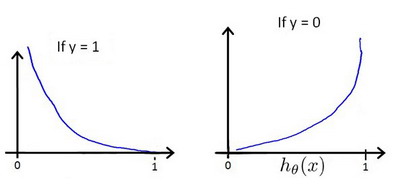
这样构建的 $Cost\left( {h_\theta}\left( x \right),y \right)$ 函数的特点是：当实际的 $y=1$ 且 ${h_\theta}\left( x \right)$ 也为 1 时误差为 0，当 $y=1$ 但  ${h_\theta}\left( x \right)$ 不为 1 时误差随着 ${h_\theta}\left( x \right)$ 变小而变大；当实际的 $y=0$ 且  ${h_\theta}\left( x \right)$ 也为 0 时代价为 0，当 $y=0$ 但  ${h_\theta}\left( x \right)$ 不为 0时误差随着 ${h_\theta}\left( x \right)$ 的变大而变大。 将构建的 $Cost\left( {h_\theta}\left( x \right),y \right)$ 简化如下：

Python代码：

import numpy as np

def cost(theta, X, y): 

  theta = np.matrix(theta)

  X = np.matrix(X)

  y = np.matrix(y)

  first = np.multiply(-y, np.log(sigmoid(X* theta.T)))

  second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))

  return np.sum(first - second) / (len(X))

这样一个代价函数，会是一个凸函数，并且没有局部最优值，我们便可以用梯度下降算法来求得能使代价函数最小的参数了。算法为：

Repeat {  $\theta_j := \theta_j - \alpha \frac{\partial}{\partial\theta_j} J(\theta)$（simultaneously update all ）}

求导后得到：

Repeat {  $\theta_j := \theta_j - \alpha \frac{1}{m}\sum\limits_{i=1}^{m}{{\left( {h_\theta}\left( \mathop{x}^{\left( i \right)} \right)-\mathop{y}^{\left( i \right)} \right)}}\mathop{x}_{j}^{(i)}$ （simultaneously update all ）}

简化代价函数

逻辑回归的代价函数：

最小化代价函数的方法，是使用梯度下降法(gradient descent)。

这就是我们通常用的梯度下降法的模板：

我们要反复更新每个参数，用这个式子来更新，就是用它自己减去学习率 $\alpha$ 乘以后面的微分项。求导后得到：

如果有 $n$ 个特征，也就是说：，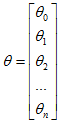

参数向量 $\theta$ 包括 ${\theta_{0}}$ ${\theta_{1}}$ ${\theta_{2}}$  一直到 ${\theta_{n}}$，就需要用这个式子：

${\theta_j}:={\theta_j}-\alpha \frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}({{x}^{(i)}})-{{y}^{(i)}}){{x}_{j}}^{(i)}}$ 来同时更新所有的 $\theta$ 值。